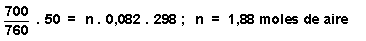, Esta cantidad se mantiene constante
a lo largo de todo el procesoLOS GASES
RESOLUCIÓN del problema nē 16:
50 litros de aire seco a 25C y 700 mm. de presión se hacen burbujear lentamente a través de agua. El aire saturado de vapor de agua sale a 20C y 1 atm. Calcular. a) Volumen final de la mezcla; b) gramos de agua evaporados; c) sí la mezcla se comprime a 20C hasta 5 atm., determinar la cantidad de agua que se condensa. - P. vapor de agua a 20C: 17, 5 mm de Hg. (Sol: a) 46,23 litros; b) 0,80 g de agua; c) 0,64 g de agua condensada.)
RESOLUCION
Cuando se hace pasar el aire a través de agua, arrastrará parte de ésta, en una cantidad tal que la presión parcial que ejerza sea su presión de vapor a esa temperatura: 20ēC, pues el aire sale saturado de agua; posteriormente, al comprimirse la mezcla a temperatura constante, la presión parcial del vapor de agua se mantendrá pues la presión de vapor depende exclusivamente de la temperatura, por todo ello, la única cantidad que permanece constante en todo el proceso es la cantidad de aire, la cual se calcula a partir de los datos iniciales:
La cantidad inicial de aire se calcula aplicándole la ecuación general de los gases ideales. Como sabemos, el aire es una mezcla por lo que no cabe hablar de su masa o peso molecular, por lo que el cálculo del número de moles, se hace suponiendo un mol "medio", y nos sale de aplicar directamente la ecuación de los gases :
P.V = n.R.T : 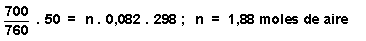, Esta cantidad se mantiene constante
a lo largo de todo el proceso
| 1,88 moles aire
0 moles de agua T = 25ēC V = 50 litros P total = 700 mm Hg |
|
1,88 moles aire
0,044 moles de agua T = 22ēC V = 46,23 litros P total = 760 mm Hg |
|
1,88 moles aire
0,0087moles de agua T = 20ēC V = 9,08 l P total = 5 atm |
P total = P parcial del aire + P vapor del agua 760 mm Hg = P parcial del aire + 17,5 mm Hg de donde
P parcial del aire = 760 - 17,5 = 742,5 mm Hg con este dato, y conocido el número de moles de aire, podemos calcular el volumen total del recipiente mediante la ecuación general de los gases ideales:
P parcial del aire.V total = n aire .R.T =>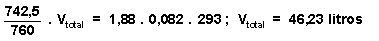
Y este
dato del volumen nos permite determinar la cantidad de vapor de agua que habrá en esta segunda etapa utilizando
la presión parcial del agua con el volumen total mediante la ecuación general de los gases ideales
P parcial del agua.V total = n agua .R.T =>
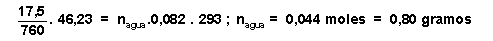
En la tercera etapa, la presión total (5 atm = 3800 mm Hg) es la suma de la presión parcial del aire más la del vapor de agua, y dado que la temperatura se mantiene a 20ēC, la presión parcial del vapor de agua seguirá siendo 17,5 mm Hg, por lo que la del aire será:
P total = P parcial del aire + P vapor del agua 3800 mm Hg = P parcial del aire + 17,5 mm Hg y así:
P parcial del aire = 3800 - 17,5 = 3782,5 mm Hg con este dato, y conocido el número de moles de aire, el cual no varía a lo largo de las tres etapas, podemos calcular el volumen total del recipiente mediante la ecuación general de los gases ideales: P parcial del aire.V total = n aire .R.T =>
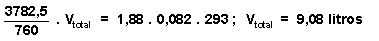y una vez calculado este volumen, se determina la
cantidad de vapor de agua que existe en el recipiente, nuevamente con la ecuación general de los gases ideales:
P parcial del agua.V total = n agua .R.T =>
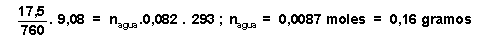por lo que la diferencia
entre la cantidad de vapor de agua que había antes y la que queda ahora, se habrá condensado:
Cantidad de agua condensada = 0,80 - 0,16 = 0,64 g de agua se condensan
