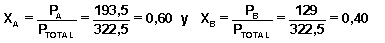
UNIVERSIDAD NACIONAL DE EDUCACIÓN A DISTANCIA

E.T.S. INGENIEROS INDUSTRIALES

QUÍMICA I - FEBRERO 2002 - 2ª SEMANA

PROBLEMA:

Un determinado volumen de una disolución equimolecular de dos líquidos A y B que se comporta como ideal, a una cierta temperatura, se la introduce en un recipiente cerrado. Se sabe que el vapor en equilibrio con la disolución es tal, que la presión parcial del componente A es 1, 5 veces mayor que la del componente B. Dicho vapor se lleva a un nuevo recipiente cerrado donde una vez licuado está en equilibrio con un segundo vapor.

La presión de vapor del líquido A puro, en las condiciones del problema, es de 387 mm de mercurio. Sabiendo que la temperatura no varia lo largo del proceso, se pide:

a) La presión de vapor del líquido puro B.

b) La presión total del primer vapor producido.

c) Las fracciones molares del segundo vapor.

Si se mezclan dos líquidos miscibles, como es el caso que nos ocupa, y la disolución se comporta como ideal, le es aplicable la ley de Raoult sobre variación de la Presión de vapor: P_{v - i} = Pº_{v -i} .X _i donde Pv _i es la presión de vapor de ese componente en la fase de vapor, Pº_{v - i} es la presión de vapor de ese componente puro y X _i es la fracción molar de ese componente en la fase líquida.

P _TOTAL = P _A + P _B siendo P _TOTAL la presión total de la mezcla gaseosa mientras que P _A + P _B son las presiones parciales de los componentes "A" y "B" en esa fase de vapor. Esta ley de las presiones parciales puede expresarse también en función de las fracciones molares (X _A y X _B respectivamente de ambos componentes en la fase de vapor, de la forma P _i = P _TOTAL . X _i .

De esta manera tendremos para este caso:

Se nos indica que la disolución es equimolecular, por lo que ambas fracciones molares serán idénticas X _A = X _B = 0,5.

Por tanto, por aplicación de la ley de Raoult para el componente A podremos conocer su

presión de vapor, la cual será:

P_{v - A} = Pº_{v -A} .X _A = 387.0,5 = 193,5 mm Hg Para determinar la presión de vapor del componente B tenemos en cuenta que se nos indica que "Se sabe que el vapor en equilibrio con la disolución es tal, que la presión parcial del componente A es 1,5 veces mayor que la del componente B" por lo que

P_{v - A} = 1,5 . P_{v -B}, de donde 193,5 = 1,5 . P_{v -B} => P_{v -B} = 129 mm Hg valor éste a partir del cual determinamos la presión de vapor del componente B puro por aplicación de la Ley de Raoult:

P_{v - B} = Pº_{v -B} .X _B ==> 129 = Pº_{v -B} .0,5 ==> Pº_{v -B} = 258 mm Hg

b) Para calcular la presión total del vapor producido , por aplicación de la Ley de Dalton de las Presiones parciales, será:

P _TOTAL = P _A + P _B = 193,5 + 129 = 322,5 mm Hg

P _TOTAL = 193,5 + 129 = 322,5 mm Hg

por lo que su composición, expresada como fracciones molares será:

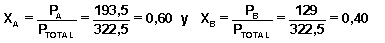
Para hacer el mismo desarrollo del problema que hemos hecho en el apartado anterior, suponemos que ese vapor se condensa todo, obteniendo una fase líquida cuya composición es X_A = 0,6 y X_B = 0,4, y dado que son dos componentes volátiles, pasarán en parte a la fase de vapor, cumpliéndose igualmente las leyes de Raoult en la disolución y de Dalton en la fase gaseosa.

Por tanto en la disolución podemos aplicarle la ley de Raoult:

P_A = Pº_A.X_A ==> P_A = 387.0,6 = 232,2 mm Hg, que será la presión de vapor del componente A en este segundo recipiente

P_B = Pº _B.X_B ==> P_B = 258.0,4 = 103,2 mm Hg, que será la presión de vapor del componente B en este segundo recipiente

La presión total en este segundo recipiente será la suma de ambas:

P _TOTAL = P _A + P _B = 232,2 + 103,2 = 335,4 mm Hg

y por tanto las correspondientes fracciones molares de ambos vapores en este segundo recipiente son:

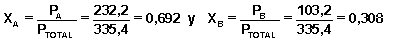
donde, como podemos observar, el vapor es más rico en el componente A (ha aumentado su fracción molar con respecto al vapor del primer recipiente) ya que este componente es más volátil (su presión de vapor es mayor).